Impose a set of behavioral state-change rules to the random arrays using Python

I was challenged by my mentor to implement the below condition using Python. 

Impose a set of behavioral state-change rules to the random arrays (100 x 100) 

Whenever a square is surrounded by 4 other squares (either adjacent or diagonal) then it retains its value for all future iterations from that point forward. 

All squares that do not become bound in any given iteration, continue changing until they are bound by 4 squares at some future time. 

The goal of this is to initiate a random array, populate it with arbitrary set of numbers from a uniform random distribution [0,1], and to apply the rules below to each square, evaluated on every iteration. 

Below is the pictorial representation of the problem 

While working on the implementation found that this condition is somewhat similar to Conway Game of life. I read some details about the Conway game of life and found it very interesting. Here are  some of the details about the Conway Game of life :

The universe of the Game of Life is an infinite two-dimensional orthogonal grid of square cells, each of which is in one of two possible states, alive or dead, or "populated" or "unpopulated" (the difference may seem minor, except when viewing it as an early model of human/urban behavior simulation or how one views a blank space on a grid). Every cell interacts with its eight neighbours, which are the cells that are horizontally, vertically, or diagonally adjacent.


I tried to implement the behavioral state-change rules using Python. While implementing took help from some of the online posts also. I tried the problem in below two ways by first taking only two states and then in the second attempt tried the rules on the random array. Here are those two approaches :

1) Took only two option of cells to be live or dead and applied the behavioral state change rule.

2) Applied behavioral state-change rules to the random arrays (100 x 100)

Here is the code for both the conditions :

Approach 1: Took only two option of cells to be live or dead and applied the behaviourial state change rule.

################################################################################

# conway-On-Off.py

#

# Author: Ravi Vijay

# 

# Description:

#

# A simple Python/matplotlib implementation of following condition :

#  Whenever a square is surrounded by 4 other squares (either adjacent or diagonal) then it retains its #value for all future iterations from that point forward.  

#  All squares that do not become bound in any given iteration, continue changing until they are #bound by 4 squares at some future time.

################################################################################

import numpy as np

import matplotlib.pyplot as plt 

import matplotlib.animation as animation

N = 100

ON = 255

OFF = 0

vals = [ON, OFF]

# populate grid with random on/off - more off than on

grid = np.random.choice(vals, N*N, p=[0.2, 0.8]).reshape(N, N)

def update(data):

  global grid

  # copy grid since we require 4 neighbors for calculation

  # Putting here the loop to go line by line 

  newGrid = grid.copy()

  for i in range(N):

    for j in range(N):

      # compute 4-neighbor sum (once adjacent & once diagonal) 

      # At boundary condition we wrap around 

      

      # Adjacent Total

      total1 = (grid[i, (j-1)%N] + grid[i, (j+1)%N] + 

               grid[(i-1)%N, j] + grid[(i+1)%N, j])/255

        

      # Diagonal Total  

      total2 = (grid[(i-1)%N, (j-1)%N] + grid[(i-1)%N, (j+1)%N] + 

               grid[(i+1)%N, (j-1)%N] + grid[(i+1)%N, (j+1)%N])/255

      

      

      # Apply rules

      if grid[i, j]  == ON:

        if (total1 !=4) or (total2 != 4):

          newGrid[i, j] = OFF

      else:

        newGrid[i, j] = ON

  # update data

  mat.set_data(newGrid)

  grid = newGrid

  return [mat]

# set up animation

fig, ax = plt.subplots()

mat = ax.matshow(grid)

ani = animation.FuncAnimation(fig, update, interval=200,

                              save_count=200)

plt.show()

Here is the screenshot for the iteration :

Approach 2: Applied behavioral state-change rules to the random arrays (100 x 100)

################################################################################

# conway.py

#

# Author: Ravi Vijay

# 

# Description:

#

# A simple Python/matplotlib implementation of following condition :

#  Whenever a square is surrounded by 4 other squares (either adjacent or diagonal) then it retains its value 

#  for all future iterations from that point forward.  

#  All squares that do not become bound in any given iteration, continue changing until they are bound by 4 squares at some future time.

################################################################################

import numpy as np

import matplotlib.pyplot as plt 

import matplotlib.animation as animation

N = 100

m=100 # Matrix Size

c=5   # Number of Colors

# populate grid with random on/off - more off than on

grid = np.random.randint(c, size=(m, m))

def update(data):

    global grid

  # copy grid since we require 8 neighbors for calculation

  # and we go line by line 

    newGrid = grid.copy()

    for i in range(m):

      for j in range(m):

      # apply rules

          if ((grid[i, (j-1)%N] == grid[i, (j+1)%N] == grid[(i-1)%N, j] == grid[(i+1)%N, j]) 

              or (grid[(i-1)%N, (j-1)%N] == grid[(i-1)%N, (j+1)%N] == grid[(i+1)%N, (j-1)%N] == grid[(i+1)%N, (j+1)%N])):

                newGrid[i, j] = grid[i,j]

                

          else:

            newGrid[i, j] = np.random.randint(c, size=(1, 1))

            

  # update data

    mat.set_data(newGrid)

    grid = newGrid

    return [mat]            

  

# set up animation

fig, ax = plt.subplots()

mat = ax.matshow(grid)

ani = animation.FuncAnimation(fig, update, interval=50,

                              save_count=50)

plt.show()

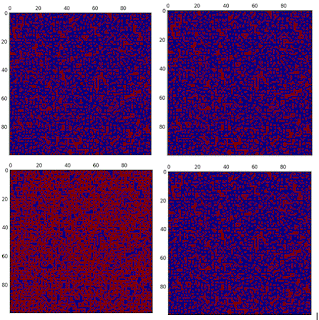
Below is the screenshot of few of the iterations :